📍 Introduction
In the world of programming and computer science, efficiency is key. We want our code to run as quickly and as smoothly as possible. This is where Big O notation comes into play. Big O notation provides a standardized way to analyze and compare the efficiency of algorithms. In this blog post, we will explore the concept of Big O notation, its significance, and how it helps us write more efficient code.
📍What is Efficiency?
Regarding programming, efficiency is all about how much computation resources are used by an algorithm. The least resources used, the more efficient algorithm is.
Generally, we only concern with only two types of resources:
Memory space needed (Space Complexity)
Time of the algorithm (Time complexity)
📍Why we need Big(O) Notation?
It seems like we do not need Big O to measure time complexity. We can use a stopwatch to calculate how long (milliseconds or seconds) an algorithm took to complete, and space complexity can be measured with KB and MB.
However, there is a huge problem with this kind of thinking.
For example, I have two computers with Intel i7 (16GB RAM) and Intel i3 (4GB RAM). So the runtime will not be the same when I run algorithm A on both devices. Obviously, the Intel i7 is more powerful than the i3 so it will solve the problem earlier.
But what if we have both computers with the same configurations? Still, the runtime will sometimes differ because other factors outside our control can influence the computer’s performance, such as concurrency and multi-processing.
To solve this issue, we analyze algorithms on paper using Big O notation for the following reasons.
Big O notation can objectively describe the efficiency of code without the use of concrete units such as (milliseconds and seconds)
Focus on how the time and space requirements scale in terms of the size of the Input.
Prepare for the worst-case scenario.
📍What is Big O?
Big O notation is a mathematical notation that describes the performance characteristics of an algorithm. It provides a way to express how the running time or space requirements of an algorithm grow relative to the input size. The "O" in Big O represents the order of growth. Big O notation focuses on the worst-case scenario or upper bound of an algorithm's performance.
📍Understanding Big O Syntax
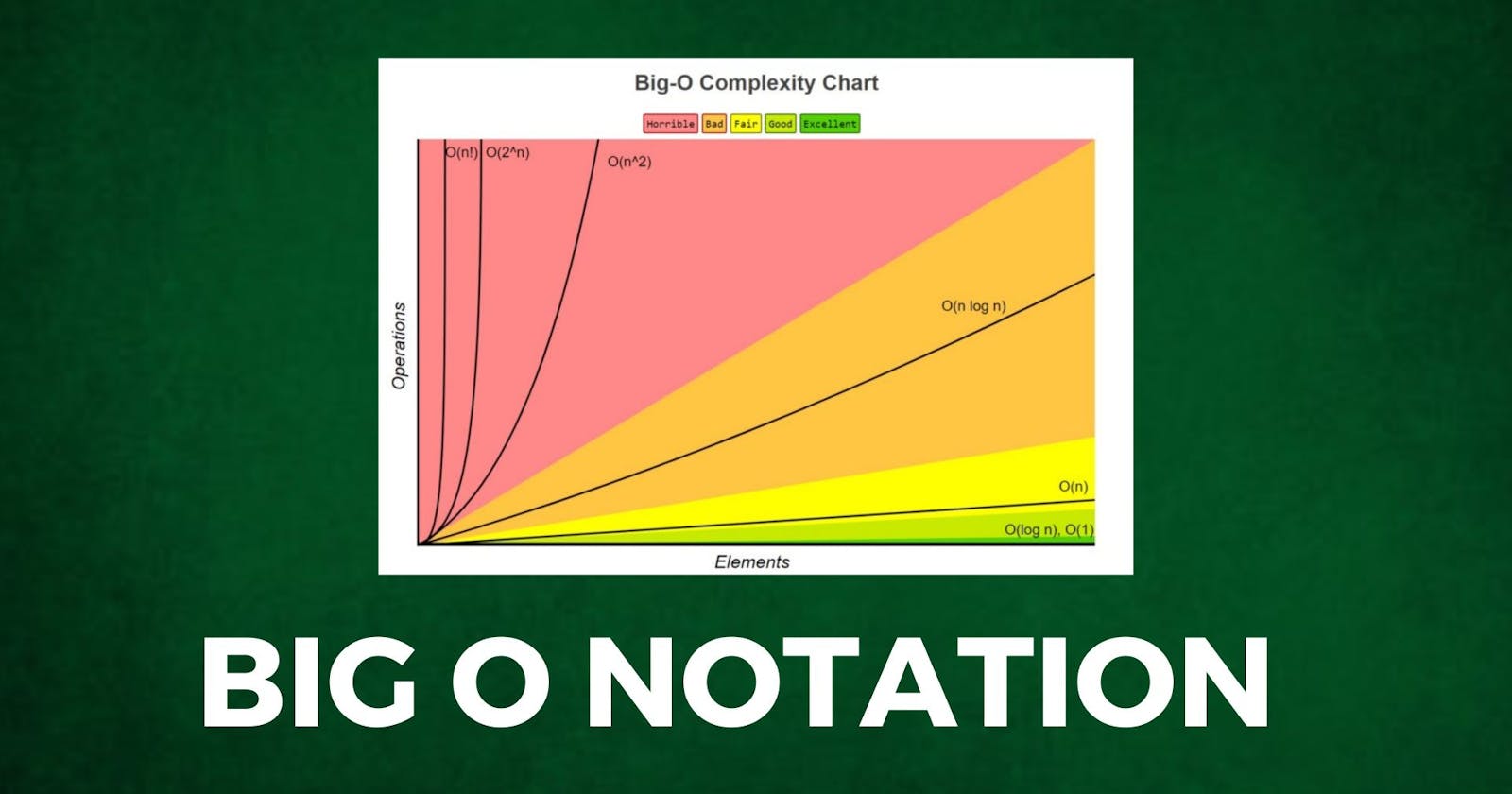
Big O notation uses various symbols to represent different growth rates. Here are some common notations you'll come across:
O(1) - Constant time complexity: The algorithm takes a fixed amount of time, regardless of the input size.
O(log n) - Logarithmic time complexity: The algorithm's runtime increases logarithmically with the input size.
O(n) - Linear time complexity: The algorithm's runtime increases linearly with the input size.
O(n^2) - Quadratic time complexity: The algorithm's runtime increases quadratically with the input size.
O(2^n) - Exponential time complexity: The algorithm's runtime grows exponentially with the input size.
The below image helps us understand the Order of Growth from Good to Bad:

📍Ignore Constants:
When we write Big O notation, we look for the fastest-growing term as the input gets larger and larger. We can simplify the equation by dropping constants and any non-dominant terms.
For example, O(2N) becomes O(N), and O(N² + N + 1000) becomes O(N²).
📍Worst Case:
Worst case means how slow/long the algorithm can run for provided input. It is recommended to consider the worst case while calculating the Big (O) Notation.
📍Time Complexity
The time complexity of an algorithm is the number of steps/iterations it takes to complete its task. Time complexity is often used to compare different algorithms, as they all have different performance characteristics.
Let's understand this with the below example:
Here's a Java function named sum that takes an integer array as input and returns the sum of its elements using a for loop
public static int sum(int[] arr) {
int N = arr.length;
int sum = 0;
for (int i = 0; i < N; i++) {
sum += arr[i];
}
return sum;
}
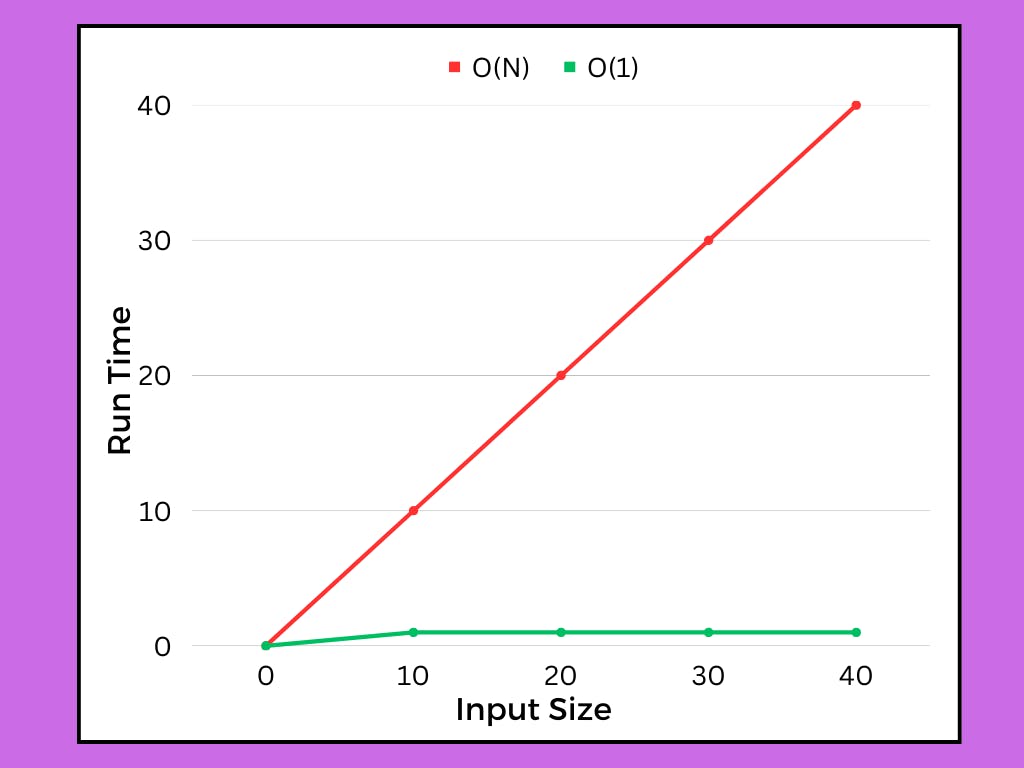
Time Complexity: The time complexity of the sum function you provided is O(n), where n is the length of the input array. The for loop iterates over each element of the array once, performing a constant amount of work (addition) for each iteration. As the size of the array increases, the number of iterations and the time taken by the loop grow linearly.
Space Complexity: The space complexity of the function is O(1), which means it uses a constant amount of additional space. Regardless of the input size, the function only requires a fixed amount of memory to store the sum variable and the loop index i.
We can represent the Linear Time Complexity O(N) and the Constant Space Complexity O(1) through the below graph:
📍Space Complexity
Space complexity is the amount of memory an algorithm uses. It’s measured in bytes, and it’s also called memory usage.
What causes space complexity?
Variables
Data Structures
Function Call
Allocations
Space complexity is more important for large data sets because they require much more memory to store than small ones do.
Let's understand this with the below example:
Here's a Java function named prefixSum that takes an integer array as input and returns an array containing the prefix sum of the input array:
Check this blog to explore the magic of prefix sum
public static int[] prefixSum(int[] arr) {
int n = arr.length;
int[] prefixSumArray = new int[n];
prefixSumArray[0] = arr[0];
for (int i = 1; i < n; i++) {
prefixSumArray[i] = prefixSumArray[i - 1] + arr[i];
}
return prefixSumArray;
}
Time Complexity: The time complexity of the prefixSum function you provided is O(n), where n is the length of the input array. The function iterates through each element of the input array once using the for loop. For each iteration, it performs a constant amount of work, which includes accessing array elements and adding them together. As the size of the input array increases, the number of iterations and the time taken by the function grow linearly.
Space Complexity: The space complexity of the function is O(n) as well. It creates a new array prefixSumArray of the same length as the input array to store the prefix sum values. The space required is directly proportional to the size of the input array.
Therefore, the time complexity is O(n) and the space complexity is O(n) for the given prefixSum function.
📍Examples of Common Big O Calculations
Big O notation is extremely helpful in choosing different sorting algorithms for different scenarios because it allows us to analyze and compare the efficiency of different algorithms in terms of their time and space complexity.
Sorting algorithms have varying time complexities, and selecting the most appropriate algorithm depends on the size of the input data and the constraints of the problem.
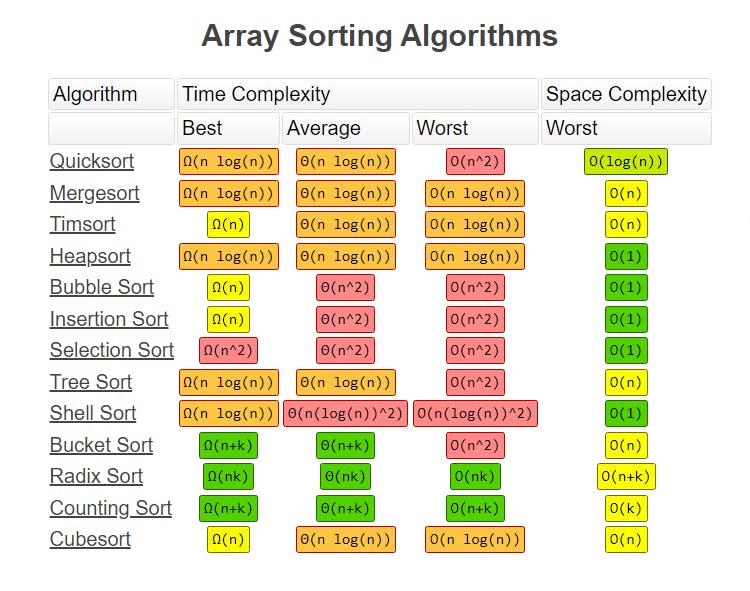
By comparing the time and space complexities and properties of different sorting algorithms, we can select the most suitable algorithm that meets the requirements of the specific scenario. Big O notation serves as a powerful tool for this purpose, allowing us to evaluate and compare the efficiency of sorting algorithms based on their expected performance with different input sizes.
📍Conclusion
Big O notation is a powerful tool in the world of programming and computer science. It provides a standardized and objective way to analyze and compare the efficiency of algorithms. By focusing on the worst-case scenario and the growth rate of an algorithm's time and space requirements, we can make informed decisions about choosing the most efficient algorithm for a given problem. Big O notation allows us to understand how algorithms scale with increasing input sizes and helps us optimize our code to run as quickly and smoothly as possible. By utilizing Big O notation, we can write more efficient code and tackle complex problems with confidence.
Hope You Find these blogs interesting and helpful I tried to share my knowledge if any Feedback or changes are required please free to contact me 😊